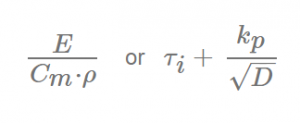Posts in category tools
Doing cool stuff with MapleTA without being a Maple expert
I have been using MapleTA for a couple of years now and so far I did not use the Maple graded question type that much. I did not feel the need and frankly I thought that my knowledge of the underlying Maple engine would be insufficient to really do a good job. But working closely with a teacher on digitizing his written exam taught me that you don’t have to be an expert user in Maple in order to create great (exam) questions in MapleTA.
A couple of months ago we started a small pilot: A teacher in Materials Science, an assessment expert and me (being the MapleTA expert) were going to recreate a previously taken, written exam into a digital format. Based on the learning goals of the course and the test blue print we wanted to create a genuine digital exam, that would take an optimal benefit of being digital and not just an online version of the same questions. The questions should reflect the skills of the students and not just assess them on the numerical values they put into the response fields.
Being so closely involved in the process and together finding essential steps and skills students need to show, really challenged me to dive into the system and come up with creative solutions mostly using the adaptive question type and maple graded questions.
Adaptive Question Type – Scenarios
The adaptive question type allowed us to create different scenario’s within a question:
- A multiple choice question was expanded into a multiple choice question (the main question) with some automatically graded underpinning questions. Students needed to answer all questions correctly in order to get the full score. Missing one question resulted in zero points. Answering the main question correctly would take the student to a set of underpinning questions. Failing on the main question, would dismiss the student from the underpinning questions and take them directly to the next question in the assignment (not having to waste time on the underpinning questions, since they needed to answer all questions correctly)
This way the chance of guessing the right answer was eliminated, resulting in not having to compensate for guessing in the overall test score. The problem itself was posed to the students in a more authentic way: Here is the situation, what steps do you need to take to get to the right solution. Posing that main question first requires the students to think about the route, without guiding them along a certain path. - A numerical question was also expanded into a main-sub question scenario. This time, when students would answer the main question correctly (requiring to find their own strategy to work towards the solution) they are taken to the next question since they’ve shown they succeeded in solving the problem. Those who did not get to the correct answer, were given a couple of additional questions, to see at what point they went wrong and thus being able to solve the problem with a little help. Still being able to gain a partial score on the main question.
- Another adaptive question scenario would require all students to go through all the main-sub questions. Using the sub questions either to underpin the main question or as a help towards the right solution by presenting the steps that need to be taken. Again allowing students to show more of their work and thoughts than a plain set of questions, without guiding students to much on ‘how to’ solve the problem.
So far the adaptive questions, but what about the maple graded?
Maple graded – formula evaluation and Preview
The exam required students to type in a lot of (non mathematical) formulas used to compute values for material properties or deriving a materials index to select the material that best performs under particular circumstances.
For example:
Maple can evaluate these type of questions quite well, since the order of different terms will not influence the outcome of the evaluation. We first tried the symbolic entry mode, but try-out sessions with students turned out that the text entry mode was to be preferred. Since it would speed up entry of the response.
Then we discovered the power of the preview button. Not only did it warn students for misspelled greek characters (e.g. lamda in stead of lambda), misplaced brackets or incorrect Maple syntax, it also allowed us to provide feedback saying that certain parameters in their response should be elaborated. This could be done by defining a Custom Previewing code, like:
if evalb(StringTools[CountCharacterOccurrences]("$RESPONSE","A")=1)
then printf("Elaborate the term A for Surface Area. ")
else printf(MathML[ExportPresentation]($RESPONSE));
end if;
This turned out to be a powerful way to reassure students their response would not be graded incorrect through syntax mistakes or not elaborating their response to the right level.
Point of attention: you need to make sure that the grading code takes into account that students might be sloppy in their use of upper and lower case characters and tend to skip subscripts if that seems insignificant to them. We used the algorithm to prepare accepted notations, writing OR statements in the grading code:
Algorithm:
$MatIndex1=maple("sigma[y]/rho/C[m]");
$MatIndex2=maple("sigma[y]/rho/c[m]");
Grading Code:
evalb(($MatIndex1)-($RESPONSE)=0) or evalb(($MatIndex2)-($RESPONSE)=0);
Through the MapleCommunity I received an alternative to compensate for the case sensitivity:
Algorithm:
$MatIndex1= "sigma[y]/rho/C[m]";
Grading Code:
evalb(parse(StringTools:-LowerCase("$RESPONSE"))=parse(StringTools:-LowerCase("$MatIndex1")));
Automatically graded ‘key-word’ questions in an adaptive section
In order to use adaptive sections in a question all questions must be graded automatically. This means you cannot pose an essay question, since it requires manual grading. We had some questions were we wanted the students to explain their choice by writing a motivation in text. Both the response to the main question and the motivation had to be correct in order to get full score. No partial grading allowed.
Having a prognosis of nearly 600 students taking this exam, the teacher obviously did not want to grade all these motivations by hand. An option would have been to use the ‘keyword’ question type that is presented in the MapleTA demo class, but since it is not a standard question type, it could not be part of an (adaptive) question designer type question. The previously mentioned Custom Preview Code inspired me to use a Maple graded question instead. Going through Metha Kamminga’s manual I found the right syntax to search for a specific string in a response text and grade the response automatically. Resulting in the following grading code:
evalb(StringTools[Search]("isolator","$RESPONSE")>=1) or
evalb(StringTools[Search]("insulator","$RESPONSE")>=1);
Naturally, the teacher should also review the responses that did not contain these key words, but certainly that would mean only having to grade a portion of the 600 student responses, since all the automatically-graded-and-found-to-be-correct would no longer need grading. Thus saving a considerable amount of time.
Preliminary conclusions of our pilot
MapleTA offers a lot of possibilities that require little or no knowledge of the Maple engine, but
- It requires careful thinking and anticipation on student behavior.
- Make sure to have your students practice the necessary notations, so they are more confident and familiar with MapleTA’s syntax or ‘whims’ as students tend to call it.
- Take your time before the exam to define the alternatives and check in detail what is excepted and what is not. This saves you a lot of time afterwards. Because unfortunately making corrections in the gradebook of MapleTA is devious, time consuming and not user friendly at all.
Handboek Digiborden
Op de blog van ICT-in-het-onderwijs vond ik een verwijzing naar een onlangs verschenen handboek digiborden. De recensie van Tessa Zadelhoff geeft een goed beeld van de inhoud.
Screencast tools
Vanmorgen vond ik onder mijn feeds van Wilfred Rubens een korte verwijzing naar een blog van Tom Kuhlmann van rapid E-learning. In de post stond een verwijzing naar een leuk en simpel screencast tool, Screenr. Met behulp van deze tool kan je in een handomdraai een screencast maken die je meteen kunt twitteren, publiceren op Youtube, etc. Inmiddels heeft Tom ook een handleiding met tips en tricks voor het maken van goede screencasts .
Zelf had ik vorige week Jing gedownload, omdat ik binnenkort aan de slag wil met screencasts voor Maple TA. Jing is iets uitgebreider, omdat je hiermee ook screenshots kan uitknippen. Dat is dan weer erg handig voor geschreven handleidingen.